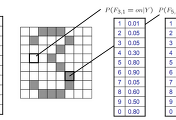
- Bayes rule
일반인이 암 환자를 진단하는 신규 검사법을 사용하여 검사해본 결과가 양성 반응일 때, 실제로 암에 걸렸을 확률을 구하는 문제가 있다고 해보겠습니다. 이 문제를 풀기 위해 주어진 조건과 조건부 확률을 다음과 같다고 가정하겠습니다.
Y -> 실제 병에 걸렸을 경우 { 1 : true, 0 : false }
X -> 검사 결과 경우 { 1 : 양성, 0 : 음성 }
P ( X = 1 | Y = 1 ) = 0.8 검사의 정확도로 실제 병에 걸렸을 경우, 검사 결과도 양성일 확률
즉, 본 검사는 80% 의 확률로 정확한 진단을 내리고 20% 확률로 실제 병이 걸린 환자에 대해 음성이라는 오진을 내리게 됩니다.
P ( X = 1 | Y = 0) = 0.1 일명 False positive 로 병이 없는데도 불구하고 검사 결과가 양성으로 나올 확률.
P ( Y = 1) = 0.004 일반적으로 암에 걸릴 확률.
조건을 확인하고 문제를 다시 읽어보도록 하겠습니다. 위와 같은 조건이 주어 졌을 때 암 검진 결과가 양성 일 경우, ( X = 1) 실제로 암에 걸렸을 확률 ( Y = 1) 이므로 우리가 구해야할 문제는 아래와 같습니다.
이 문제는 베이즈 정리를 이용해 풀 수 있습니다. 베이즈 정리의 기본 공식은 다음과 같습니다.
공식으로 확인해 봐도 알겠지만 베이즈 정리는 본래 역확률 (inverse problem) 을 해결하기 위해 사용되는 방법 입니다. P(B|A) 라는 조건부 확률을 알고 있을 때 P(A|B) 를 구하는 방법인 것 입니다. 하지만 공식처럼 단순히 역확률 문제에만 사용되는 것이 아니라 이전 경험을 바탕으로 확률을 추론하는데 사용할 수 있는 방법 이기도 합니다. 주어진 자료를 이용해 새로운 사실의 확률을 구하는 방법, 다시 말해 머신러닝에 사용되기 매우 좋은 방법 입니다.
앞의 문제는 암 검진 결과가 양성일 때 실제 암에 걸렸을 확률을 구하라는 것이었습니다. 주어진 조건을 공식에 맞추어 문제를 풀어도록 하겠습니다.
머신 러닝의 관점에서 베이즈 정리를 다룰 때 몇가지 알아야할 용어도 있습니다. 위 조건에서 P(Y) 는 암에 걸릴 확률 입니다. 어떠한 자료도 없을 때 특정 사건이 일어날 확률에 대한 가정으로 사전 확률(Prior Probability) 이란 용어가 있습니다. 그리고 가능도(likelihood) 라는 용어도 있습니다. 사건이 일어났다는 가정 하에서 새로이 가지게 된 자료가 관측될 확률을 의미 합니다. 베이즈 정리의 분모는 가능도를 구할때 조건으로 걸린 사건의 확률입니다. 마지막으로 위 문제에서 답에 해당 하는 부분, 사전확률과 가능도를 이용해 구한 답을 사후 확률(posterior probability) 라고 합니다.
사실 위의 문제의 경우 사건의 종류가 단 2개 뿐인 매우 간단한 문제 였습니다. 일반적인 문제나 실제 머신 러닝 적용을 위한 문제에서는 사건의 경우는 2개 이상을 것 입니다. n개의 사건을 가지는 일반적인 베이즈 정리는 다음과 같습니다.
표본 공간 는 서로소인
의 합집합이며
는
위에서 정의된 사건 일때
아래의 그림과 함께 공식을 보시면 더 이해하기 쉬우실 것 같습니다. P(A1|B) 를 구하고 싶다면 조건부 확률의 공식에 따라 분자는 P(A1∩B) 를, 분모는 P(B) 를 가지게 됩니다. 곱셈정리에 따라 분자와 분모는 각각 위의 공식과 같이 변환 되는 것 입니다.
'ML' 카테고리의 다른 글
| ML 101 : 서포트 벡터 머신(Support Vector Machine, SVM) - Margin (0) | 2017.03.20 |
|---|---|
| ML101 : 나이브 베이즈 (Naive Bayes) : 분류 (1) | 2017.03.13 |
| ML101 : weka practical exercise / 의사결정트리 (2) (0) | 2017.02.28 |
| ML 101 : weka practical exercise / 의사결정트리 (1) (0) | 2017.02.15 |
| ML 101 : 머신러닝 무료 강의 모음 (1) | 2017.02.07 |